14. Wavelet-Stat Tool
14.1. Introduction
The Wavelet-Stat tool decomposes two-dimensional forecasts and observations according to intensity and scale. This section describes the Wavelet-Stat tool, which enables users to apply the Intensity-Scale verification technique described by Casati et al. (2004).
The Intensity-Scale technique is one of the recently developed verification approaches that focus on verification of forecasts defined over spatial domains. Spatial verification approaches, as opposed to point-by-point verification approaches, aim to account for the presence of features and for the coherent spatial structure characterizing meteorological fields. Since these approaches account for the intrinsic spatial correlation existing between nearby grid-points, they do not suffer from point-by-point comparison related verification issues, such as double penalties. Spatial verification approaches aim to account for the observation and forecast time-space uncertainties, and aim to provide feedback on the forecast error in physical terms.
The Intensity-Scale verification technique, as most of the spatial verification approaches, compares a forecast field to an observation field. To apply the Intensity-Scale verification approach, observations need to be defined over the same spatial domain of the forecast to be verified.
Within the spatial verification approaches, the Intensity-Scale technique belongs to the scale-decomposition (or scale-separation) verification approaches. The scale-decomposition approaches enable users to perform the verification on different spatial scales. Weather phenomena on different scales (e.g. frontal systems versus convective showers) are often driven by different physical processes. Verification on different spatial scales can therefore provide deeper insights into model performance at simulating these different processes.
The spatial scale components are obtained usually by applying a single band spatial filter to the forecast and observation fields (e.g. Fourier, Wavelets). The scale-decomposition approaches measure error, bias and skill of the forecast on each different scale component. The scale-decomposition approaches therefore provide feedback on the scale dependency of the error and skill, on the no-skill to skill transition scale, and on the capability of the forecast of reproducing the observed scale structure.
The Intensity-Scale technique evaluates the forecast skill as a function of the intensity values and of the spatial scale of the error. The scale components are obtained by applying a two dimensional Haar wavelet filter. Note that wavelets, because of their locality, are suitable for representing discontinuous fields characterized by few sparse non-zero features, such as precipitation. Moreover, the technique is based on a categorical approach, which is a robust and resistant approach, suitable for non-normally distributed variables, such as precipitation. The intensity-scale technique was specifically designed to cope with the difficult characteristics of precipitation fields, and for the verification of spatial precipitation forecasts. However, the intensity-scale technique can also be applied to verify other variables, such as cloud fraction.
14.2. Scientific and statistical aspects
14.2.1. The method
Casati et al. (2004) applied the Intensity-Scale verification to preprocessed and re-calibrated (unbiased) data. The preprocessing was aimed to mainly normalize the data, and defined categorical thresholds so that each categorical bin had a similar sample size. The recalibration was performed to eliminate the forecast bias. Preprocessing and recalibration are not strictly necessary for the application of the Intensity-Scale technique. The MET Intensity-Scale Tool does not perform either, and applies the Intensity-Scale approach to biased forecasts, for categorical thresholds defined by the user.
The Intensity Scale approach can be summarized in the following 5 steps:
For each threshold, the forecast and observation fields are transformed into binary fields: where the grid-point precipitation value meets the threshold criteria it is assigned 1, where the threshold criteria are not met it is assigned 0. This can also be done with no thresholds indicated at all and in that case the grid-point values are not transformed to binary fields and instead the raw data is used as is for statistics. Figure 14.1 illustrates an example of a forecast and observation fields, and their corresponding binary fields for a threshold of 1mm/h. This case shows an intense storm of the scale of 160 km displaced almost its entire length. The displacement error is clearly visible from the binary field difference and the contingency table image obtained for the same threshold Table 14.1.
The binary forecast and observation fields obtained from the thresholding are then decomposed into the sum of components on different scales, by using a 2D Haar wavelet filter (Figure 14.3). Note that the scale components are fields, and their sum adds up to the original binary field. For a forecast defined over square domain of \(\mathbf{2^n} **x** :math:\)mathbf{2^n} grid-points, the scale components are n+1: n mother wavelet components + the largest father wavelet (or scale-function) component. The n mother wavelet components have resolution equal to 1, 2, 4, … \(\mathbf{2^{n-1}}\) grid-points. The largest father wavelet component is a constant field over the \(\mathbf{2^n} **x** :math:\)mathbf{2^n} grid-point domain with value equal to the field mean.
Note that the wavelet transform is a linear operator: this implies that the difference of the spatial scale components of the binary forecast and observation fields (Figure 14.3) are equal to the spatial scale components of the difference of the binary forecast and observation fields (Figure 14.2), and these scale components also add up to the original binary field difference (Figure 14.1). The intensity-scale technique considers thus the spatial scale of the error. For the case illustrated (Figure 14.1 and Figure 14.2) note the large error associated at the scale of 160 km, due the storm, 160km displaced almost its entire length.
Note also that the means of the binary forecast and observation fields (i.e. their largest father wavelet components) are equal to the proportion of forecast and observed events above the threshold, (a+b)/n and (a+c)/n, evaluated from the contingency table counts (Table 14.1) obtained from the original forecast and observation fields by thresholding with the same threshold used to obtain the binary forecast and observation fields. This relation is intuitive when observing forecast and observation binary fields and their corresponding contingency table image (Figure 14.1). The comparison of the largest father wavelet component of binary forecast and observation fields therefore provides feedback on the whole field bias.
For each threshold (t) and for each scale component (j) of the binary forecast and observation, the Mean Squared Error (MSE) is then evaluated (Figure 14.4). The error is usually large for small thresholds, and decreases as the threshold increases. This behavior is partially artificial, and occurs because the smaller the threshold the more events will exceed it, and therefore the larger would be the error, since the error tends to be proportional to the amount of events in the binary fields. The artificial effect can be diminished by normalization: because of the wavelet orthogonal properties, the sum of the MSE of the scale components is equal to the MSE of the original binary fields: \(MSE(t) = j MSE(t,j)\). Therefore, the percentage that the MSE for each scale contributes to the total MSE may be computed: for a given threshold, t, \({MSE\%}(t,j) = {MSE}(t,j)/ {MSE}(t)\). The MSE% does not exhibit the threshold dependency, and usually shows small errors on large scales and large errors on small scales, with the largest error associated to the smallest scale and highest threshold. For the NIMROD case illustrated, note the large error at 160 km and between the thresholds of and 4 mm/h, due to the storm, 160km displaced almost its entire length.
Note that the MSE of the original binary fields is equal to the proportion of the counts of misses (c/n) and false alarms (b/n) for the contingency table (Table 14.1) obtained from the original forecast and observation fields by thresholding with the same threshold used to obtain the binary forecast and observation fields: \({MSE}(t)=(b+c)/n\). This relation is intuitive when comparing the forecast and observation binary field difference and their corresponding contingency table image (Table 14.1).
The MSE for the random binary forecast and observation fields is estimated by \({MSE}(t) {random}= {FBI}*{Br}*(1-{Br}) + {Br}*(1- {FBI}*{Br})\), where \({FBI}=(a+b)/(a+c)\) is the frequency bias index and \({Br}=(a+c)/n\) is the sample climatology from the contingency table (Table 14.1) obtained from the original forecast and observation fields by thresholding with the same threshold used to obtain the binary forecast and observation fields. This formula follows by considering the Murphy and Winkler (1987) framework, applying the Bayes’ theorem to express the joint probabilities b/n and c/n as product of the marginal and conditional probability (e.g. Jolliffe and Stephenson, 2012; Wilks, 2010), and then noticing that for a random forecast the conditional probability is equal to the unconditional one, so that b/n and c/n are equal to the product of the corresponding marginal probabilities solely.
For each threshold (t) and scale component (j), the skill score based on the MSE of binary forecast and observation scale components is evaluated (Figure 14.5). The standard skill score definition as in Jolliffe and Stephenson (2012) or Wilks (2010) is used, and random chance is used as reference forecast. The MSE for the random binary forecast is equipartitioned on the n+1 scales to evaluate the skill score: \({SS} (t,j)=1- {MSE}(t,j)*(n+1)/ {MSE}(t) {random}\)
The Intensity-Scale (IS) skill score evaluates the forecast skill as a function of the precipitation intensity and of the spatial scale of the error. Positive values of the IS skill score are associated with a skillful forecast, whereas negative values are associated with no skill. Usually large scales exhibit positive skill (large scale events, such as fronts, are well predicted), whereas small scales exhibit negative skill (small scale events, such as convective showers, are less predictable), and the smallest scale and highest thresholds exhibit the worst skill. For the NIMROD case illustrated note the negative skill associated with the 160 km scale, for the thresholds to 4 mm/h, due to the 160 km storm displaced almost its entire length.
Forecast |
Observation |
Total |
|
|---|---|---|---|
o = 1 (e.g., “Yes”) |
o = 0 (e.g., “No”) |
||
f = 1 (e.g., “Yes”) |
Hits = a |
False Alarms = b |
a+b |
f = 0 (e.g., “No”) |
Misses = c |
Correct rejections = d |
c+d |
Total |
a+c |
b+d |
a+b+c+d |
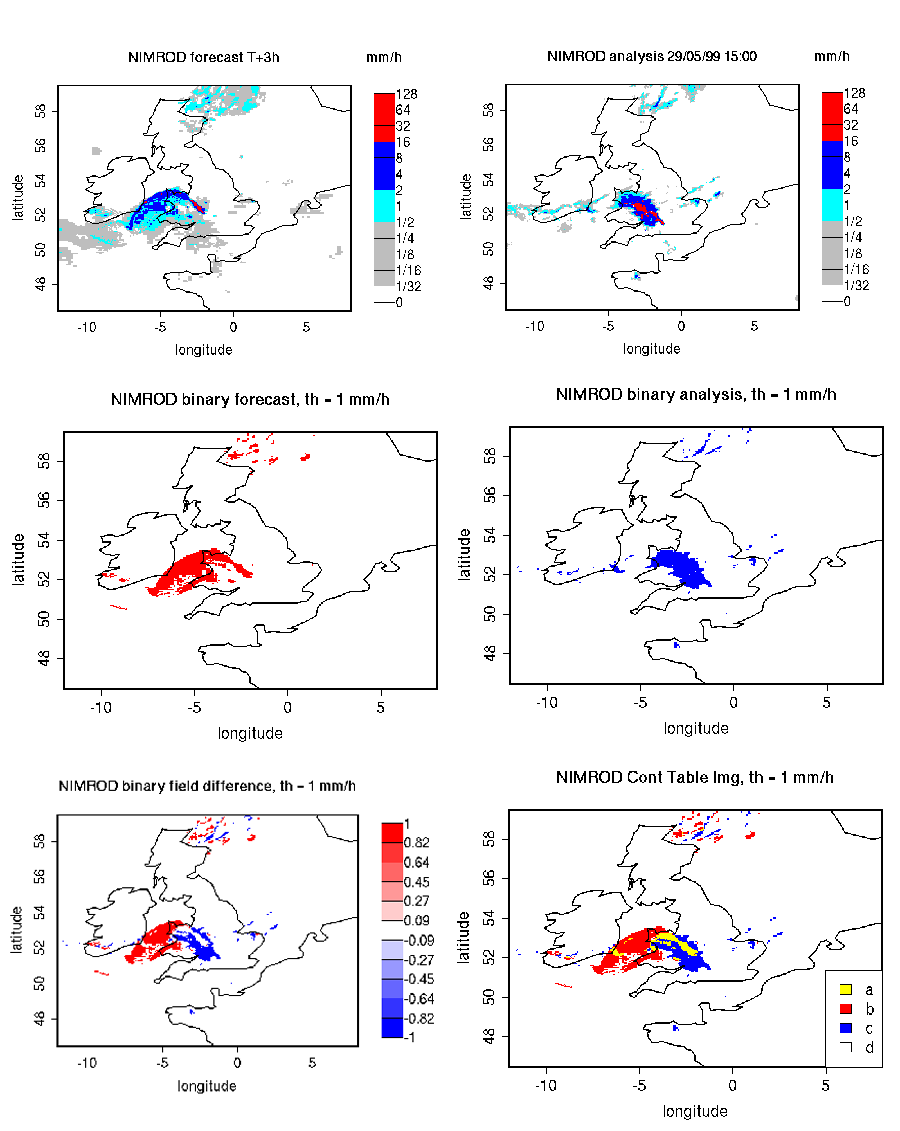
Figure 14.1 NIMROD 3h lead-time forecast and corresponding verifying analysis field (precipitation rate in mm/h, valid the 05/29/99 at 15:00 UTC); forecast and analysis binary fields obtained for a threshold of 1mm/h, the binary field difference has their corresponding Contingency Table Image (see Table 14.1). The forecast shows a storm of 160 km displaced almost its entire length.
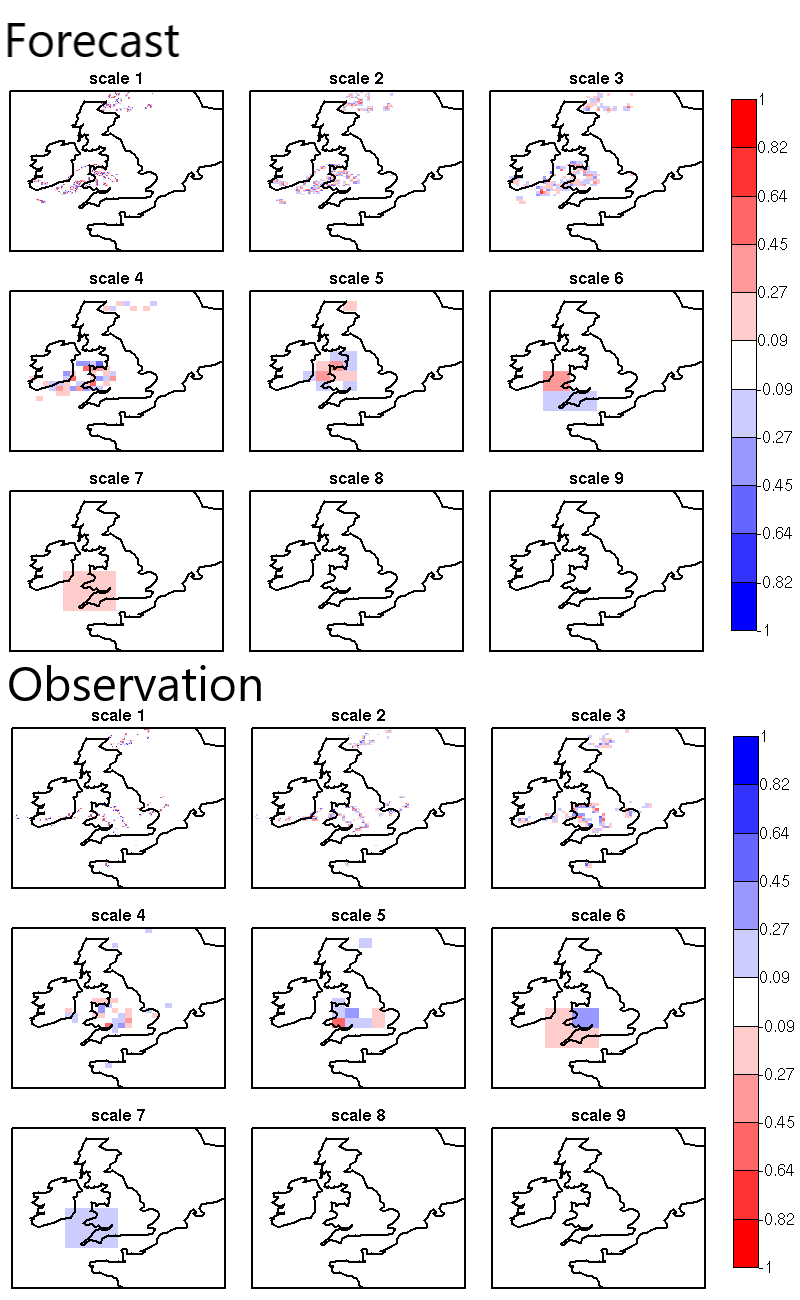
Figure 14.2 NIMROD binary forecast (top) and binary analysis (bottom) spatial scale components obtained by a 2D Haar wavelet transform (th=1 mm/h). Scales 1 to 8 refer to mother wavelet components (5, 10, 20, 40, 80, 160, 320, 640 km resolution); scale 9 refers to the largest father wavelet component (1280 km resolution).
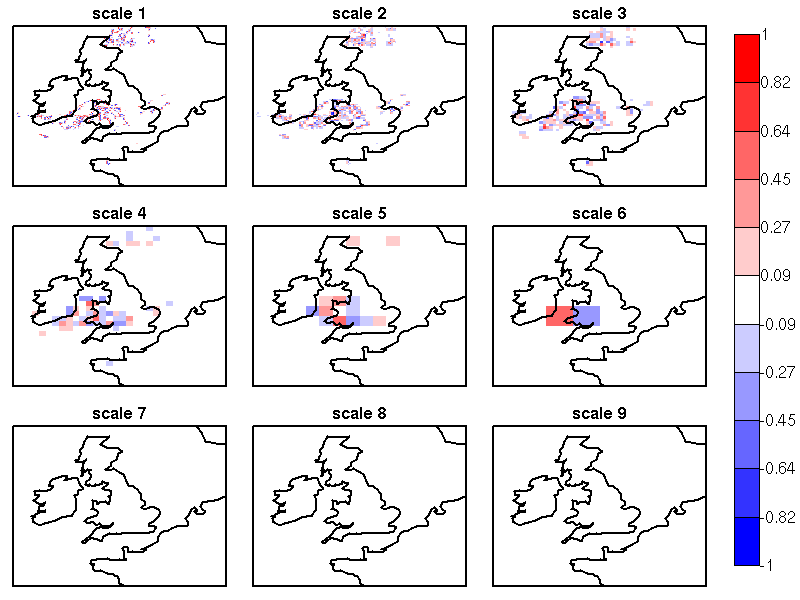
Figure 14.3 NIMROD binary field difference spatial scale components obtained by a 2D Haar wavelet transform (th=1 mm/h). Scales 1 to 8 refer to mother wavelet components (5, 10, 20, 40, 80, 160, 320, 640 km resolution); scale 9 refers to the largest father wavelet component (1280 km resolution). Note the large error at the scale 6 = 160 km, due to the storm, 160 km displaced almost of its entire length.
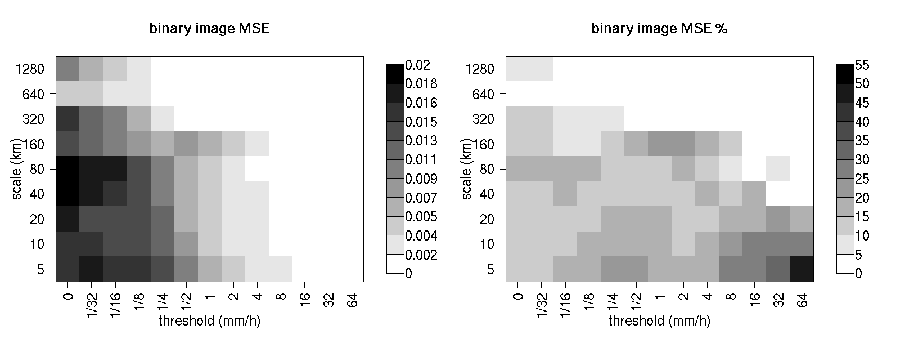
Figure 14.4 MSE and MSE % for the NIMROD binary forecast and analysis spatial scale components. In the MSE%, note the large error associated with the scale 6 = 160 km, for the thresholds ½ to 4 mm/h, associated with the displaced storm.
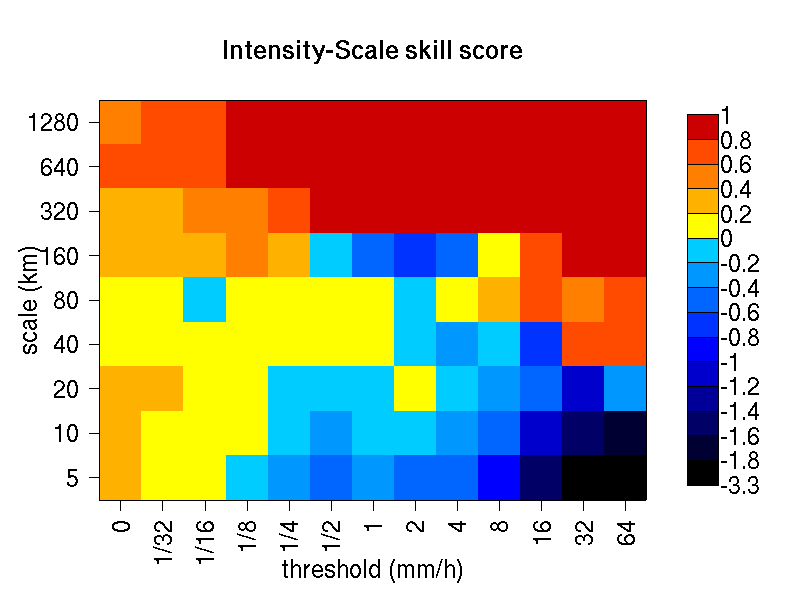
Figure 14.5 Intensity-Scale skill score for the NIMROD forecast and analysis shown in Figure 14.1. The skill score is a function of the intensity of the precipitation rate and spatial scale of the error. Note the negative skill associated with the scale 6 = 160 km, for the thresholds to 4 mm/h, associated with the displaced storm.
In addition to the MSE and the SS, the energy squared is also evaluated, for each threshold and scale (Figure 14.6). The energy squared of a field X is the average of the squared values: \({En2}(X)= \sum_i x_i^2\). The energy squared provides feedback on the amount of events present in the forecast and observation fields for each scale, for a given threshold. Usually, small thresholds are associated with a large energy, since many events exceed the threshold. Large thresholds are associated with a small energy, since few events exceed the threshold. Comparison of the forecast and observed squared energy provide feedback on the bias on different scales, for each threshold.
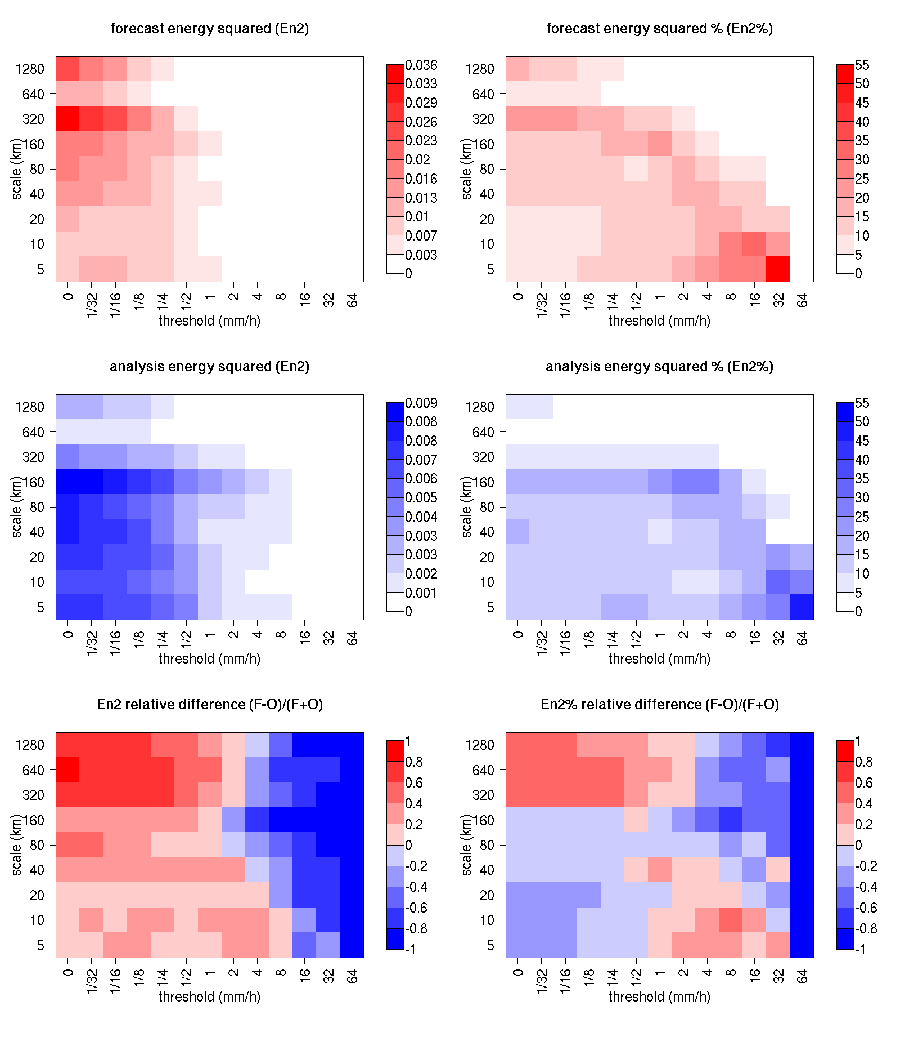
Figure 14.6 Energy squared and energy squared percentages, for each threshold and sale, for the NIMROD forecast and analysis, and forecast and analysis En2 and En2% relative differences.
The En2 bias for each threshold and scale is assessed by the En2 relative difference, equal to the difference between forecast and observed squared energies normalized by their sum: \({En2}(F)- {En2}(O)]/[{En2}(F)+ {En2}(O)]\). Since defined in such a fashion, the En2 relative difference accounts for the difference between forecast and observation squared energies relative to their magnitude, and it is sensitive therefore to the ratio of the forecast and observed squared energies. The En2 relative difference ranges between -1 and 1, positive values indicate over-forecast and negative values indicate under-forecast. For the NIMROD case illustrated the forecast exhibits over-forecast for small thresholds, quite pronounced on the large scales, and under-forecast for high thresholds.
As for the MSE, the sum of the energy of the scale components is equal to the energy of the original binary field: \({En2}(t) = j \ {En2}(t,j)\). Therefore, the percentage that the En2 for each scale contributes the total En2 may be computed: for a given threshold, t, \({En2\%}(t,j) = {En2}(t,j)/ {En2}(t)\). Usually, for precipitation fields, low thresholds exhibit most of the energy percentage on large scales (and less percentage on the small scales), since low thresholds are associated with large scale features, such as fronts. On the other hand, for higher thresholds, the energy percentage is usually larger on small scales, since intense events are associated with small scales features, such as convective cells or showers. The comparison of the forecast and observation squared energy percentages provides feedback on how the events are distributed across the scales, and enables the comparison of forecast and observation scale structure.
For the NIMROD case illustrated, the scale structure is assessed again by the relative difference, but calculated of the squared energy percentages. For small thresholds the forecast overestimates the number of large scale events and underestimates the number of small scale events, in proportion to the total number of events. On the other hand, for larger thresholds the forecast underestimates the number of large scale events and overestimates the number of small scale events, again in proportion to the total number of events. Overall it appears that the forecast overestimates the percentage of events associated with high occurrence, and underestimates the percentage of events associated with low occurrence. The En2% for the 64 mm/h thresholds is homogeneously underestimated for all the scales, since the forecast does not have any event exceeding this threshold.
Note that the energy squared of the observation binary field is identical to the sample climatology \({Br}=(a+c)/n\). Similarly, the energy squared of the forecast binary field is equal to \((a+b)/n\). The ratio of the squared energies of the forecast and observation binary fields is equal to the \({FBI}=(a+b)/(a+c)\), for the contingency table (Table 14.1) obtained from the original forecast and observation fields by thresholding with the same threshold used to obtain the binary forecast and observation fields.
14.2.2. The spatial domain constraints
The Intensity-Scale technique is constrained by the fact that orthogonal wavelets (discrete wavelet transforms) are usually performed dyadic domains, square domains of \(\mathbf{2^n} **x** :math:\)mathbf{2^n} grid-points. The Wavelet-Stat tool handles this issue based on settings in the configuration file by defining tiles of dimensions \(\mathbf{2^n} **x** :math:\)mathbf{2^n} over the input domain in the following ways:
User-Defined Tiling: The user may define one or more tiles of size \(\mathbf{2^n} **x** :math:\)mathbf{2^n} over their domain to be applied. This is done by selecting the grid coordinates for the lower-left corner of the tile(s) and the tile dimension to be used. If the user specifies more than one tile, the Intensity-Scale method will be applied to each tile separately. At the end, the results will automatically be aggregated across all the tiles and written out with the results for each of the individual tiles. Users are encouraged to select tiles which consist entirely of valid data.
Automated Tiling: This tiling method is essentially the same as the user-defined tiling method listed above except that the tool automatically selects the location and size of the tile(s) to be applied. It figures out the maximum tile of dimension \(\mathbf{2^n} **x** :math:\)mathbf{2^n} that fits within the domain and places the tile at the center of the domain. For domains that are very elongated in one direction, it defines as many of these tiles as possible that fit within the domain.
Padding: If the domain size is only slightly smaller than \(\mathbf{2^n} **x** :math:\)mathbf{2^n}, for certain variables (e.g. precipitation), it is advisable to expand the domain out to \(\mathbf{2^n} **x** :math:\)mathbf{2^n} grid-points by adding extra rows and/or columns of fill data. For precipitation variables, a fill value of zero is used. For continuous variables, such as temperature, the fill value is defined as the mean of the valid data in the rest of the field. A drawback to the padding method is the introduction of artificial data into the original field. Padding should only be used when a very small number of rows and/or columns need to be added.
14.2.3. Aggregation of statistics on multiple cases
The Stat-Analysis tool aggregates the intensity scale technique results. Since the results are scale-dependent, it is sensible to aggregate results from multiple model runs (e.g. daily runs for a season) on the same spatial domain, so that the scale components for each singular case will be the same number, and the domain, if not a square domain of \(\mathbf{2^n} **x** :math:\)mathbf{2^n} grid-points, will be treated in the same fashion. Similarly, the intensity thresholds for each run should all be the same.
The MSE and forecast and observation squared energy for each scale and thresholds are aggregated simply with a weighted average, where weights are proportional to the number of grid-points used in each single run to evaluate the statistics. If the same domain is always used (and it should) the weights result all the same, and the weighted averaging is a simple mean. For each threshold, the aggregated Br is equal to the aggregated squared energy of the binary observation field, and the aggregated FBI is obtained as the ratio of the aggregated squared energies of the forecast and observation binary fields. From aggregated Br and FBI, the MSErandom for the aggregated runs can be evaluated using the same formula as for the single run. Finally, the Intensity-Scale Skill Score is evaluated by using the aggregated statistics within the same formula used for the single case.
14.3. Practical information
The following sections describe the usage statement, required arguments and optional arguments for the Stat-Analysis tool.
14.3.1. wavelet_stat usage
The usage statement for the Wavelet-Stat tool is shown below:
Usage: wavelet_stat
fcst_file
obs_file
config_file
[-outdir path]
[-log file]
[-v level]
[-compress level]
wavelet_stat has three required arguments and accepts several optional ones.
14.3.1.1. Required arguments for wavelet_stat
The fcst_file argument is the gridded file containing the model data to be verified.
The obs_file argument is the gridded file containing the observations to be used.
The config_file argument is the configuration file to be used. The contents of the configuration file are discussed below.
14.3.1.2. Optional arguments for wavelet_stat
The -outdir path indicates the directory where output files should be written.
The -log file option directs output and errors to the specified log file. All messages will be written to that file as well as standard out and error. Thus, users can save the messages without having to redirect the output on the command line. The default behavior is no log file.
The -v level option indicates the desired level of verbosity. The contents of “level” will override the default setting of 2. Setting the verbosity to 0 will make the tool run with no log messages, while increasing the verbosity will increase the amount of logging.
The -compress level option indicates the desired level of compression (deflate level) for NetCDF variables. The valid level is between 0 and 9. The value of “level” will override the default setting of 0 from the configuration file or the environment variable MET_NC_COMPRESS. Setting the compression level to 0 will make no compression for the NetCDF output. Lower number is for fast compression and higher number is for better compression.
An example of the wavelet_stat calling sequence is listed below:
wavelet_stat \
sample_fcst.grb \
sample_obs.grb \
WaveletStatConfig
In the example, the Wavelet-Stat tool will verify the model data in the sample_fcst.grb GRIB file using the observations in the sample_obs.grb GRIB file applying the configuration options specified in the WaveletStatConfig file.
14.3.2. wavelet_stat configuration file
The default configuration file for the Wavelet-Stat tool, WaveletStatConfig_default, can be found in the installed share/met/config directory. Another version of the configuration file is provided in scripts/config. We recommend that users make a copy of the default (or other) configuration file prior to modifying it. The contents are described in more detail below.
Note that environment variables may be used when editing configuration files, as described in the Section 5.1.1.
model = "WRF";
desc = "NA";
obtype = "ANALYS";
fcst = { ... }
obs = { ... }
regrid = { ... }
mask_missing_flag = NONE;
met_data_dir = "MET_BASE";
ps_plot_flag = TRUE;
fcst_raw_plot = { color_table = "MET_BASE/colortables/met_default.ctable";
plot_min = 0.0; plot_max = 0.0; }
obs_raw_plot = { ... }
wvlt_plot = { ... }
output_prefix = "";
version = "VN.N";
The configuration options listed above are common to many MET tools and are described in Section 5.
// Empty list of thresholds
cat_thresh = [];
// Or explicitly set the NA threshold type
cat_thresh = [>0.0, >=5.0, NA];
The cat_thresh option defines an array of thresholds for each field defined in the fcst and obs dictionaries. The number of forecast and observation categorical thresholds must match. If set to an empty list, the thresholds will not be applied (no binary masking) and all the raw grid-point values will be used for downstream statistics.
If the array of thresholds is an empty list, the application will set the threshold to NA internally and skip applying the thresholds. If the threshold is set to NA explicitly in the list, the application will also skip applying the threshold.
Since the application has the ability to loop through multiple thresholds (for multiple fields), a user can include NA in the list of thresholds to produce statistics for the raw data values for the given field.
grid_decomp_flag = AUTO;
tile = {
width = 0;
location = [ { x_ll = 0; y_ll = 0; } ];
}
The grid_decomp_flag variable specifies how tiling should be performed:
AUTO indicates that the automated-tiling should be done.
TILE indicates that the user-defined tiles should be applied.
PAD indicated that the data should be padded out to the nearest dimension of \(\mathbf{2^n} **x** :math:\)mathbf{2^n}
The width and location variables allow users to manually define the tiles of dimension they would like to apply. The x_ll and y_ll variables specify the location of one or more lower-left tile grid (x, y) points.
wavelet = {
type = HAAR;
member = 2;
}
The wavelet_flag and wavelet_k variables specify the type and shape of the wavelet to be used for the scale decomposition. The Casati et al. (2004) method uses a Haar wavelet which is a good choice for discontinuous fields like precipitation. However, users may choose to apply any wavelet family/shape that is available in the GNU Scientific Library. Values for the wavelet_flag variable, and associated choices for k, are described below:
HAAR for the Haar wavelet (member = 2).
HAAR_CNTR for the Centered-Haar wavelet (member = 2).
DAUB for the Daubechies wavelet (member = 4, 6, 8, 10, 12, 14, 16, 18, 20).
DAUB_CNTR for the Centered-Daubechies wavelet (member = 4, 6, 8, 10, 12, 14, 16, 18, 20).
BSPLINE for the Bspline wavelet (member = 103, 105, 202, 204, 206, 208, 301, 303, 305, 307, 309).
BSPLINE_CNTR for the Centered-Bspline wavelet (member = 103, 105, 202, 204, 206, 208, 301, 303, 305, 307, 309).
output_flag = {
isc = BOTH;
}
The output_flag array controls the type of output that the Wavelet-Stat tool generates. This flag is set similarly to the output flag of the other MET tools, with possible values of NONE, STAT, and BOTH. The ISC line type is the only one available for Intensity-Scale STAT lines.
nc_pairs_flag = {
latlon = TRUE;
raw = TRUE;
}
The nc_pairs_flag is described in Section 12.3.2
14.3.3. wavelet_stat output
wavelet_stat produces output in STAT and, optionally, ASCII and NetCDF and PostScript formats. The ASCII output duplicates the STAT output but has the data organized by line type. While the Wavelet-Stat tool currently only outputs one STAT line type, additional line types may be added in future releases. The output files are written to the default output directory or the directory specified by the -outdir command line option.
The output STAT file is named using the following naming convention:
wavelet_stat_PREFIX_HHMMSSL_YYYYMMDD_HHMMSSV.stat where PREFIX indicates the user-defined output prefix, HHMMSS indicates the forecast lead time, and YYYYMMDD_HHMMSS indicates the forecast valid time.
The output ASCII files are named similarly:
wavelet_stat_PREFIX_HHMMSSL_YYYYMMDD_HHMMSSV_TYPE.txt where TYPE is isc to indicate that this is an intensity-scale line type.
The format of the STAT and ASCII output of the Wavelet-Stat tool is similar to the format of the STAT and ASCII output of the Point-Stat tool. Please refer to the tables in Section 11.3.3 for a description of the common output for STAT files types. The information contained in the STAT and isc files are identical. However, for consistency with the STAT files produced by other tools, the STAT file will only have names for the header columns. The isc file contains names for all columns. The format of the ISC line type is explained in the following table.
HEADER |
||
|---|---|---|
Column Number |
Header Column Name |
Description |
1 |
VERSION |
Version number |
2 |
MODEL |
User provided text string designating model name |
3 |
DESC |
User provided text string describing the verification task |
4 |
FCST_LEAD |
Forecast lead time in HHMMSS format |
5 |
FCST_VALID_BEG |
Forecast valid start time in YYYYMMDD_HHMMSS format |
6 |
FCST_VALID_END |
Forecast valid end time in YYYYMMDD_HHMMSS format |
7 |
OBS_LEAD |
Observation lead time in HHMMSS format |
8 |
OBS_VALID_BEG |
Observation valid start time in YYYYMMDD_HHMMSS format |
9 |
OBS_VALID_END |
Observation valid end time in YYYYMMDD_HHMMSS format |
10 |
FCST_VAR |
Model variable |
11 |
FCST_UNITS |
Units for model variable |
12 |
FCST_LEV |
Selected Vertical level for forecast |
13 |
OBS_VAR |
Observation variable |
14 |
OBS_UNITS |
Units for observation variable |
15 |
OBS_LEV |
Selected Vertical level for observations |
16 |
OBTYPE |
User provided text string designating the observation type |
17 |
VX_MASK |
Verifying masking region indicating the masking grid or polyline region applied |
18 |
INTERP_MTHD |
NA in Wavelet-Stat |
19 |
INTERP_PNTS |
NA in Wavelet-Stat |
20 |
FCST_THRESH |
The threshold applied to the forecast |
21 |
OBS_THRESH |
The threshold applied to the observations |
22 |
COV_THRESH |
NA in Wavelet-Stat |
23 |
ALPHA |
NA in Wavelet-Stat |
24 |
LINE_TYPE |
See table below. |
ISC OUTPUT FORMAT |
||
|---|---|---|
Column Number |
ISC Column Name |
Description |
24 |
ISC |
Intensity-Scale line type |
25 |
TOTAL |
The number of grid points (forecast locations) used |
26 |
TILE_DIM |
The dimensions of the tile |
27 |
TILE_XLL |
Horizontal coordinate of the lower left corner of the tile |
28 |
TILE_YLL |
Vertical coordinate of the lower left corner of the tile |
29 |
NSCALE |
Total number of scales used in decomposition |
30 |
ISCALE |
The scale at which all information following applies |
31 |
MSE |
Mean squared error for this scale |
32 |
ISC |
The intensity scale skill score |
33 |
FENERGY |
Forecast energy squared for this scale |
34 |
OENERGY |
Observed energy squared for this scale |
35 |
BASER |
The base rate (not scale dependent) |
36 |
FBIAS |
The frequency bias |
The Wavelet-Stat tool creates a NetCDF output file containing the raw and decomposed values for the forecast, observation, and difference fields for each combination of variable and threshold value.
The dimensions and variables included in the wavelet_stat NetCDF files are described in Tables Table 14.4 and Table 14.5.
wavelet_stat NetCDF DIMENSIONS |
|
|---|---|
NetCDF Dimension |
Description |
x |
Dimension of the tile which equals \(\mathbf{2^n}\) |
y |
Dimension of the tile which equals \(\mathbf{2^n}\) |
scale |
Dimension for the number of scales. This is set to n+2, where \(\mathbf{2^n}\) is the tile dimension. The 2 extra scales are for the binary image and the wavelet averaged over the whole tile. |
tile |
Dimension for the number of tiles used |
wavelet-stat NetCDF VARIABLES |
||
|---|---|---|
NetCDF Variable |
Dimension |
Description |
FCST_FIELD_LEVEL_RAW |
tile, x, y |
Raw values for the forecast field specified by “FIELD_LEVEL” |
OBS_FIELD_LEVEL_RAW |
tile, x, y |
Raw values for the observation field specified by “FIELD_LEVEL” |
DIFF_FIELD_LEVEL_RAW |
tile, x, y |
Raw values for the difference field (f-o) specified by “FIELD_LEVEL” |
FCST_FIELD_LEVEL_THRESH |
tile, scale, x, y |
Wavelet scale-decomposition of the forecast field specified by “FIELD_LEVEL_THRESH” |
OBS_FIELD_LEVEL_THRESH |
tile, scale, x, y |
Wavelet scale-decomposition of the observation field specified by “FIELD_LEVEL_THRESH” |
Lastly, the Wavelet-Stat tool creates a PostScript plot summarizing the scale-decomposition approach used in the verification. The PostScript plot is generated using internal libraries and does not depend on an external plotting package. The generation of this PostScript output can be disabled using the ps_plot_flag configuration file option.
The PostScript plot begins with one summary page illustrating the tiling method that was applied to the domain. The remaining pages depict the Intensity-Scale method that was applied. For each combination of field, tile, and threshold, the binary difference field (f-o) is plotted followed by the difference field for each decomposed scale. Underneath each difference plot, the statistics applicable to that scale are listed. Examples of the PostScript plots can be obtained by running the example cases provided with the MET tarball.