21. MODE Time Domain Tool
21.1. Introduction
21.1.1. Motivation
MODE Time Domain (MTD) is an extension of the MODE object-based approach to verification. In addition to incorporating spatial information, MTD utilizes the time dimension to get at temporal aspects of forecast verification. Since the two spatial dimensions of traditional meteorological forecasts are retained in addition to the time dimension, the method is inherently three dimensional. Given that, however, the overall methodology has deliberately been kept as similar as possible to that of traditional MODE.
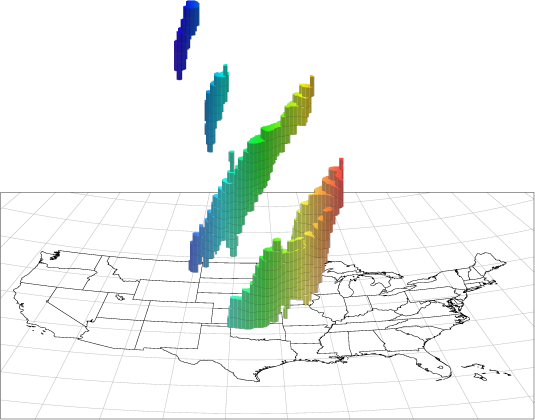
Figure 21.1 MTD Spacetime Objects
A plot of some MTD precipitation objects is shown over the United States in Figure 21.1. The colors indicate longitude, with red in the east moving through the spectrum to blue in the west. Time increases vertically in this plot (and in most of the spacetime diagrams in this users’ guide). A few things are worthy of note in this figure. First, the tendency of storm systems to move from west to east over time shows up clearly. Second, tracking of storm objects over time is easily done: if we want to know if a storm at one time is a later version of a storm at an earlier time, we need only see if they are part of the same 3D spacetime object. Lastly, storms splitting up or merging over time are handled easily by this method.
The 2D (or traditional) MODE approach to object-base verification enabled users to analyze forecasts in terms of location errors, intensity errors and shape, size and orientation errors. MTD retains all of that capability, and adds new classes of forecast errors involving time information: speed and direction errors, buildup and decay errors, and timing and duration errors. This opens up new ways of analyzing forecast quality.
In the past, many MET users have performed separate MODE runs at a series of forecast valid times and analyzed the resulting object attributes, matches and merges as functions of time in an effort to incorporate temporal information in assessments of forecast quality. MTD was developed as a way to address this need in a more systematic way. Most of the information obtained from such multiple coordinated MODE runs can be obtained more simply from MTD.
At first glance, the addition of a third dimension would seem to entail no difficulties other than increased memory and processing requirements to handle the three-dimensional datasets and objects, and that would indeed be largely true of an extension of MODE that used three spatial dimensions. In fact, the implementation of MTD entailed both conceptual difficulties (mostly due to the fact that there is no distance function in spacetime, so some MODE attributes, such as centroid distance, no longer even made sense), and engineering difficulties brought on by the need to redesign several core MODE algorithms for speed. It is planned that in the future some of these improved algorithms will be incorporated into MODE.
In this section, we will assume that the reader has a basic familiarity with traditional MODE, its internal operation, (convolution thresholding, fuzzy logic matching and merging) and its output. We will not review these things here. Instead, we will point out differences in MTD from the way traditional MODE does things when they come up. This release is a beta version of MTD, intended mostly to encourage users to experiment with it and give us feedback and suggestions to be used in a more robust MTD release in the future.
21.2. Scientific and Statistical Aspects
21.2.1. Attributes
Object attributes are, for the most part, calculated in much the same way in MTD as they are in MODE, although the fact that one of the dimensions is non-spatial introduces a few quirks. Several of the object attributes that traditional MODE calculates assume that distances, angles and areas can be calculated in grid coordinates via the usual Euclidean/Cartesian methods. That is no longer the case in spacetime, since there is no distance function (more precisely, no metric) there. Given two points in this spacetime, say \((x_1, y_1, t_1)\) and \((x_2, y_2, t_2)\), there is no way to measure their separation with a single nonnegative number in a physically meaningful way. If all three of our dimensions were spatial, there would be no difficulties.
This means that some care must be taken both in determining how to generalize the calculation of a geometric attribute to three-dimensional spacetime, and also in interpreting the attributes even in the case where the generalization is straightforward.
21.2.2. Convolution
As in MODE, MTD applies a convolution filter to the raw data as a preliminary step in resolving the field into objects. The convolution step in MTD differs in several respects from that performed in MODE, however.
First, MTD typically reads in several planes of data for each data field-one plane for each time step, and there is really no limit to the number of time steps. So MTD is convolving much more data than it would be if it were simply analyzing a 2D data field. Secondly, MTD convolves in time as well as space, which again increases the amount of data needing to be processed. The net effect of all this is to greatly increase the time needed to perform the convolution step.
Because of this, the developers decided to make several changes in the way convolution was performed in MTD. Most of the differences come from the need to make the convolution step as fast as possible.
The most basic change is to use a square convolution filter rather than the circular one that MODE uses. The overall “size” of the filter is still determined by one parameter (denoted \(R\), as in MODE), but this should not be thought of as a radius. Instead, the size of the square is \((2 R + 1) \times (2 R + 1)\), as shown in Figure 21.2.
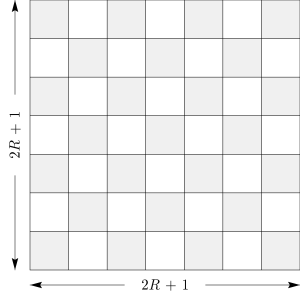
Figure 21.2 Convolution Region
Another change is that we do not allow any bad data in the convolution square. In MODE, the user may specify what percentage of bad data in the convolution region is permissible, and it will rescale the value of the filter accordingly for each data point. For the sake of speed, MTD requires that there be no bad data in the convolution region. If any bad data exists in the region, the convolved value there is set to a bad data flag.
21.2.3. 3D Single Attributes
MTD calculates several 3D attributes for single objects. The object could come from either the forecast field or the observed field.
A 3D spacetime centroid \((\bar{x}, \bar{y}, \bar{t})\) is calculated. There are no statistical overtones here. The number \(\bar{x}\), for example, is just the average value of the \(x\) coordinate over the object.
The vector velocity \((v_x, v_y)\) is obtained by fitting a line to a 3D object. The requirement for fitting the line is to minimize the sum of the squares of the spatial distances from each point of the object to the line to be minimized. (We can’t measure distances in spacetime but at each fixed time t we can measure purely spatial distances.) See Figure 21.3 for an illustration, where the solid line is the fitted axis, and the inclination of the axis from the vertical is a measure of object speed. Thus, from this velocity we get the speed and direction of movement of the object. As in MODE, where spatial separation is in units of the grid resolution, so here in MTD the unit of length is the grid resolution, and the unit of time is whatever the time separation between the input files is. Speed and velocity are thus in grid units per time unit.
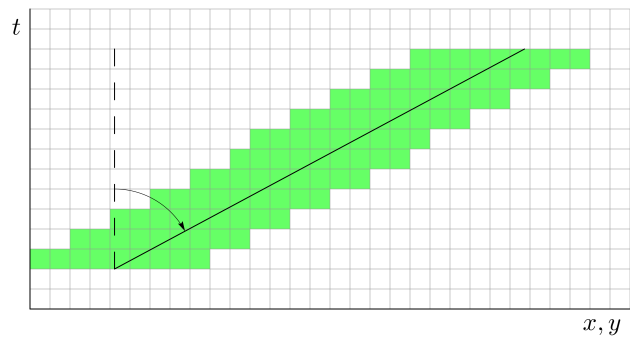
Figure 21.3 Velocity
The spatial orientation of an object (what traditional MODE calls the axis angle of an object) is gotten by fitting a plane to an object. As with the case of velocity, our optimization criterion is that the sum of the squares of the spatial distances from each point of the object to the plane be minimized.
Figure 21.4 gives some idea of the reason for fitting a plane, rather than a line, as MODE does. On the left in the figure, we see an object (in blue shaped like an “A”) at several time steps moving through the grid. For simplicity, the object is not rotating as it moves (though of course real objects can certainly do this). At each time step, the 2D MODE spatial axis of the object is indicated by the red line. In the center of the figure, we see the same thing, just with more time steps. And on the right, even more time steps. We see that the axis lines at each time step sweep out a plane in three dimensions, shown in red on the right. This plane is the same one that MTD would calculate for this 3D object to determine its spatial orientation, i.e., axis angle. Indeed, for the special case of an object that is not moving at all, the MTD calculation of axis angle reduces to the same one that traditional MODE uses, as it should.
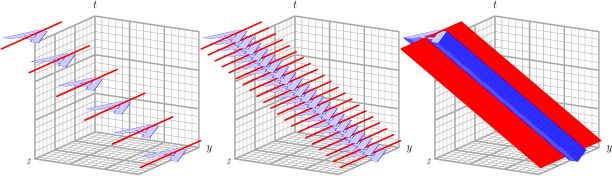
Figure 21.4 3D axis
A simple integer count of the number of grid squares in an object for all of it’s lifetime gives the volume of the object. Remember that while we’re working in three dimensions, one of the dimensions is non-spatial, so one should not attempt to convert this to a volume in, e.g., \(\text{km}^3\).
The start time and end time of an object are attributes as well. These are integers reflecting at which time step an object starts and ends. These values are zero-based, so for example, if an object comes into existence at the \(\text{3}^{rd}\) time step and lasts until the \(\text{9}^{th}\) time step, then the start time and end time will be listed as 2 and 8, respectively. Note that this object has a lifetime of 7 time steps, not 6.
Centroid distance traveled is the total great circle distance, in kilometers, traveled by the 2D spatial centroid over the lifetime of the object. In other words, at each time \(t\) for which the 3D object exists, the set of points in the object also have that value of \(t\) will together form a 2D spatial object. That 2D object will have a spatial centroid, which will move around as \(t\) varies. This attribute represents this total 2D centroid movement over time.
Finally, MTD calculates several intensity percentiles of the raw data values inside each object. Not all of the attributes are purely geometrical.
21.2.4. 3D Pair Attributes
The next category of spatial attributes is for pairs of objects - one of the pair coming from the collection of forecast objects, the other coming from the observation objects.
Note: whenever a pair attribute is described below as a delta, that means it’s a simple difference of two single-object attributes. The difference is always taken as “forecast minus observed”.
The spatial centroid distance is the purely spatial part of the centroid separation of two objects. If one centroid is at \((\bar{x}_1, \bar{y}_1, \bar{t}_1)\) and the other is at \((\bar{x}_2, \bar{y}_2, \bar{t}_2)\) then the distance is calculated as
The time centroid delta is the difference between the time coordinates of the centroid. Since this is a simple difference, it can be either positive or negative.
The axis difference is smaller of the two angles that the two spatial axis planes make with each other. Figure 21.5 shows the idea. In the figure, the axis angle would be reported as angle \(\alpha\), not angle \(\beta\).
Speed delta and direction difference are obtained from the velocity vectors of the two objects. Speed delta is the difference in the lengths of the vectors, and direction difference is the angle that the two vectors make with each other.
Volume ratio is the volume of the forecast object divided by the volume of the observed object. Note that any 3D object must necessarily have a nonzero volume, so there’s no chance of zeros in the denominator.
Start time delta and end time delta are the differences in the corresponding time steps associated with the two objects and are computed as “forecast minus obs”.
Intersection volume measures the overlap of two objects. If the two objects do not overlap, then this will be zero.
Duration difference is the difference in the lifetimes of the two objects constituting the pair, in the sense of “forecast minus obs”. For example, if the forecast object of the pair has a lifetime of 5 time steps, and the observed object has a lifetime of 3 time steps, then this attribute has the value 2. Note that we do not take absolute values of the difference, so this attribute can be positive, negative, or zero.
Finally, the total interest gives the result of the fuzzy-logic matching and merging calculation for this pair of objects. Note that this is provided only for simple objects, not for clusters.
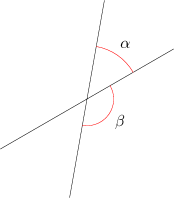
Figure 21.5 Axis Angle Difference
21.2.5. 2D Constant-Time Attributes
The final category of object attributes calculated by MTD are two-dimensional spatial attributes for horizontal (i.e., constant-time) slices of a spacetime object. This is so that the behavior of these attributes over time can be examined. These 2D constant-time attributes are written out for both simple and cluster objects.
For example, in our earlier discussion relating to Figure 21.4, we mentioned that for simplicity, the object in the figure was not allowed to rotate as it moved. But what if the object (a hurricane, for example) is rotating over time? In that case, it’s probably not meaningful to assign a single spatial orientation to the object over its entire lifetime. If we had a spatial axis angle at each time, however, then we could fit a model such as \(\theta = \theta_0 + \omega t\) to the angles and test the goodness of fit.
For such reasons, having 2D spatial attributes (as in MODE) for each object at each time step can be useful. The list of the 2D attributes calculated is:
◦ Centroid \((x, y)\)
◦ Centroid latitude and longitude
◦ Area
◦ Axis Angle
21.2.6. Matching and Merging
Matching and merging operations in MTD are done in a simpler fashion than in MODE. In order to understand this operation, it is necessary to discuss some very basic notions of graph theory.
A graph is a finite set of vertices (also called nodes) and edges, with each edge connecting two vertices. Conceptually, it is enough for our purposes to think of vertices as points and edges as lines connecting them. See Figure 21.6 for an illustration. In the figure we see a collection of 11 nodes, indicated by the small circles, together with some edges indicated by straight line segments. A path is a sequence of vertices \((v_1, v_2, \ldots, v_n)\) such that for each \(1 \leq i < n\) there is an edge connecting \(v_i\) to \(v_{i + 1}\). For example, in Figure 21.6, there is no edge connecting vertices #6 and #7, but there is a path connecting them. In illustrations, graph vertices are often labelled with identifying information, such as the numbers in Figure 21.6.
If we consider two distinct nodes in a graph to be related if there is a path connecting them, then it’s easy to see that this defines an equivalence relation on the set of nodes, partitioning the graph into equivalence classes. Any node, such as #10 in Figure 21.6, that has no edges emanating from it is in a class by itself.
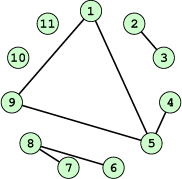
Figure 21.6 Basic Graph Example
We have barely scratched the surface of the enormous subject of graph theory, but this will suffice for our purposes. How does MTD use graphs? Essentially the simple forecast and observed objects become nodes in a graph. Each pair of objects that have sufficiently high total interest (as determined by the fuzzy logic engine) generates an edge connecting the two corresponding nodes in the graph. The graph is then partitioned into equivalence classes using path connectivity (as explained above), and the resulting equivalence classes determine the matches and merges.
An example will hopefully make this clear. In parts (a) and (b) of Figure 21.7 we indicate the objects in the forecast and observed field for this simple example. We have used 2D rather than 3D objects in this example for simplicity. Also, to help distinguish the objects in each field, the forecast objects are labelled by numbers and the observed object by letters. Each forecast and each observed object become nodes in a graph as indicated in part (c) of the figure.
For the purposes of this example, suppose that the MTD fuzzy engine reports that observed simple object B and forecast simple object 4 together have a total interest higher than the total interest threshold specified in the config file. Also, observed simple object C and forecast simple object 4 have high enough interest to pass the threshold. Furthermore, forecast simple objects 2 and 3 both have sufficiently high interest when paired with observed simple object A.
These four pairings result in the 4 edges in the graph shown by the solid lines in part (c) of the figure. Partitioning this graph into equivalence classes results in the three sets indicated in part (d) of the figure. These three sets are the cluster objects determined by MTD. In this example, forecast objects 2 and 3 are merged into forecast cluster object #1 which is matched to observed cluster object #1, consisting of observed object A. (As in MODE, a cluster object may contain multiple simple objects, but may also consist of a single simple object.) Essentially, forecast simple objects 2 and 3 are merged because there is a path connecting them in the graph. This is indicated by the dashed line in the graph.
Continuing this example, forecast cluster object #2 (consisting only of forecast simple object 4) is matched to observed cluster object #2 (consisting of observed simple objects B and C). Again, the merging of observed simple objects is indicated by the dashed line in the graph.
Forecast cluster object #3 consists solely of forecast simple object 1. It is not matched to any observed cluster object. Alternatively, one may take the viewpoint that forecast simple object 1 ended up not participating in the matching and merging process; it is not merged with anything, it is not matched with anything. Essentially it represents a false alarm.
To summarize: Any forecast simple objects that find themselves in the same equivalence class are merged. Similarly, any observed objects in the same class are merged. Any forecast and observed objects in the same class are matched.
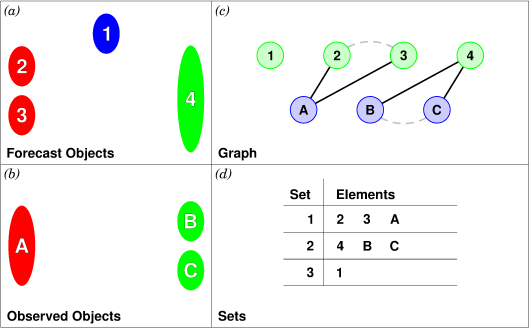
Figure 21.7 Match & Merge Example
21.3. Practical Information
21.3.1. MTD Input
The formats for two-dimensional data files used as input to MTD are the same ones supported by most of the MET tools. Generally speaking, if MODE can use a forecast or observation data file as input, then that file can also be used by MTD. The only difference is that while MODE takes only one forecast and one observed data file as input, MTD takes a series of files.
As shown in the next section, filenames for each time used must be given. Thus, for example, if MTD is being used for verification over a period of 24 hours, and the data file valid times are separated by one hour, then a total of 48 filenames must be specified on the MTD command line - 24 filenames for the forecast files, and 24 for the observation files. Further, the filenames must be given in order of increasing valid time. Many users will prefer to write scripts to automate this, rather than type in a lengthy command line by hand.
21.3.2. MTD Usage
The usage statement for the MODE-TD tool is listed below: The command line switches may be given in any order.
Usage: mtd
-fcst file_1 ... file_n | file_list
-obs file_1 ... file_n | file_list
-single file_1 ... file_n | file_list
-config config_file
[-outdir path]
[-log file]
[-v level]
The MODE-TD tool has three required arguments and can accept several optional arguments.
21.3.2.1. Required Arguments for mtd
-fcst file_list gives a list of forecast 2D data files to be processed by MTD. The files should have equally-spaced intervals of valid time.
-obs file_list gives a list of observation 2D data files to be processed by MTD. As with the {cb -fcst} option, the files should have equally-spaced intervals of valid time. This valid time spacing should be the same as for the forecast files.
-config config_file gives the path to a local configuration file that is specific to this particular run of MTD. The default MTD configuration file will be read first, followed by this one. Thus, only configuration options that are different from the default settings need be specified. Options set in this file will override any corresponding options set in the default configuration file.
21.3.2.2. Optional Arguments for mtd
-single file_list may be used instead of -fcst and -obs to define objects in a single field.
-log file gives the name of a file where a log of this MTD run will be written. All output that appears on the screen during a MTD run will be duplicated in the log file.
-v level gives the verbosity level. As with the -log option described above, this option is present in most of the MET tools. Increasing this value causes more diagnostic output to be written to the screen (and also to the log file, if one has been specified).
-outdir path gives the name of the directory into which MTD will write its output files. If not specified, then MTD will write its output into the current directory.
An example of the mtd calling sequence is listed below:
mtd -fcst fcst_files/*.grb \
-obs obs_files/*.grb \
-config MTDConfig_default \
-outdir out_dir/mtd \
-v 1
In this example, the MODE-TD tool will read in a list of forecast GRIB files in the fcst_files directory and similarly spaced observation GRIB files in the obs_files directory. It uses a configuration file called MTDConfig_default and writes the output to the out_dir/mtd directory.
21.3.3. MTD Configuration File
The default configuration file for the MODE tool, MODEConfig_default, can be found in the installed share/met/config directory. Another version of the configuration file is provided in scripts/config. We encourage users to make a copy of the configuration files prior to modifying their contents.Most of the entries in the MTD configuration file should be familiar from the corresponding file for MODE. This initial beta release of MTD does not offer all the tunable options that MODE has accumulated over the years, however. In this section, we will not bother to repeat explanations of config file details that are exactly the same as those in MODE; we will only explain those elements that are different from MODE, and those that are unique to MTD.
model = "FCST";
desc = "NA";
obtype = "ANALYS";
regrid = { ... }
met_data_dir = "MET_BASE";
output_prefix = "";
version = "VN.N";
The configuration options listed above are common to many MET tools and are described in Section 5.
grid_res = 4;
fcst = {
field = {
name = "APCP";
level = "A03";
}
conv_time_window = { beg = -1; end = 1; }
conv_radius = 60.0/grid_res; // in grid squares
conv_thresh = >=5.0;
}
obs = fcst;
total_interest_thresh = 0.7;
The configuration options listed above are common to many MODE and are described in Section 19.3.2.
The conv_time_window entry is a dictionary defining how much smoothing in time should be done. The beg and end entries are integers defining how many time steps should be used before and after the current time. The default setting of beg = -1; end = 1; uses one time step before and after. Setting them both to 0 effectively disables smoothing in time.
inten_perc_value = 99;
The inten_perc_value entry is an integer between 0 and 100 which specifies a requested intensity percentile value. By default, MTD writes 5 output columns for the 10th, 25th, 50th, 75th, and 90th percentile of object intensities. The percentile value specified here indicates which percentile should be written to the 6th output column.
min_volume = 2000;
The min_volume entry tells MTD to throw away objects whose “volume” (as described elsewhere in this section) is smaller than the given value. Spacetime objects whose volume is less than this will not participate in the matching and merging process, and no attribute information will be written to the ASCII output files. The default value is 10,000. If this seems rather large, consider the following example: Suppose the user is running MTD on a \(600 \times 400\) grid, using 24 time steps. Then the volume of the whole data field is 600 \(\times\) 400 \(\times\) 24 = 5,760,000 cells. An object of volume 10,000 represents only 10,000/5,760,000 = 1/576 of the total data field. Setting min_volume too small will typically produce a very large number of small objects, slowing down the MTD run and increasing the size of the output files.The configuration options listed above are common to many MODE and are described in Section 19.3.2.
weight = {
space_centroid_dist = 1.0;
time_centroid_delta = 1.0;
speed_delta = 1.0;
direction_diff = 1.0;
volume_ratio = 1.0;
axis_angle_diff = 1.0;
start_time_delta = 1.0;
end_time_delta = 1.0;
}
The weight entries listed above control how much weight is assigned to each pairwise attribute when computing a total interest value for object pairs. See Table 21.4 for a description of each weight option. When the total interest value is computed, the weighted sum is normalized by the sum of the weights listed above.
interest_function = {
space_centroid_dist = ( ... );
time_centroid_delta = ( ... );
speed_delta = ( ... );
direction_diff = ( ... );
volume_ratio = ( ... );
axis_angle_diff = ( ... );
start_time_delta = ( ... );
end_time_delta = ( ... );
};
The interest_function entries listed above control how much weight is assigned to each pairwise attribute when computing a total interest value for object pairs. See Table 21.4 for a description of each weight option. The interest functions may be defined as a piecewise linear function or as an algebraic expression. A piecewise linear function is defined by specifying the corner points of its graph. An algebraic function may be defined in terms of several built-in mathematical functions. See Section 19.2 for how interest values are used by the fuzzy logic engine. By default, many of these functions are defined in terms of the previously defined grid_res entry.
nc_output = {
latlon = true;
raw = true;
object_id = true;
cluster_id = true;
};
The nc_output dictionary contains a collection of boolean flags controlling which fields are written to the NetCDF output file. latlon controls the output of a pair of 2D fields giving the latitude and longitude of each grid point. The raw entry controls the output of the raw input data for the MTD run. These will be 3D fields, one for the forecast data and one for the observation data. Finally, the object_id and cluster_id flags control the output of the object numbers and cluster numbers for the objects. This is similar to MODE.
txt_output = {
attributes_2d = true;
attributes_3d = true;
};
The txt_output dictionary also contains a collection of boolean flags, in this case controlling the output of ASCII attribute files. The attributes_2d flag controls the output of the 2D object attributes for constant-time slices of 3D objects, while the attributes_3d flag controls the output of single and pair 3D spacetime object attributes.
21.3.4. mtd Output
MTD creates several output files after each run in ASCII and NetCDF formats. There are text files giving 2D and 3D attributes of spacetime objects and information on matches and merges, as well as a NetCDF file giving the objects themselves, in case any further or specialized analysis of the objects needs to be done.
MODE, along with several other of the MET tools (wavelet_stat for example, and a few others), provides PostScript-based graphics output to help visualize the output. Unfortunately, no similar graphics capabilities are provided with MTD, mainly because of the complexity of producing 3D plots. This should not discourage the user from making their own plots, however. There is enough information in the various output files created by MTD to make a wide variety of plots. Highly motivated users who write their own plotting scripts are encouraged to submit them to the user-contributed code area of the MET website. Due credit will be given, and others will benefit from their creations.
ASCII output
Five ASCII output files are created:
Single attributes for 3D simple objects
Single attributes for 3D cluster objects
Pair attributes for 3D simple objects
Pair attributes for 3D cluster objects
2D spatial attributes for single simple objects for each time index of their existence.
Each ASCII file is laid out in tabular format, with the first line consisting of text strings giving names for each column. The first 15 columns of each file are identical, and give information on timestamps, model names, and the convolution radius and threshold used for the forecast and observation input data.
These columns are explained in Table 21.1. Each file contains additional columns that come after these. Columns for 2D constant-time attributes are shown in Table 21.2. Columns for 3D single and pair attributes are shown in Table 21.3 and Table 21.4 respectively.
The contents of the OBJECT_ID and OBJECT_CAT columns identify the objects using the same logic as the MODE tool. In these columns, the F and O prefixes are used to indicate simple forecast and observation objects, respectively. Similarly, the CF and CO prefixes indicate cluster forecast and observation objects, respectively. Each prefix is followed by a 3-digit number, using leading zeros, to indicate the object number (as in F001, O001, CF001, or CO000). Pairs of objects are indicated by listing the forecast object information followed by the observation object information, separated by an underscore (as in F001_O001 or CF001_CO001). The OBJECT_ID column indicates the single object or pair of objects being described in that line. The OBJECT_CAT column indicates the cluster or pair of clusters to which these object(s) belong. A simple object that is not part of a cluster is assigned a cluster number of zero (as in CF000 or CO000). When pairs of objects belong to the same matching cluster, the OBJECT_CAT column indicates the matching cluster number (as in CF001_CO001). When they do not, the OBJECT_CAT column is set to CF000_CO000.
HEADER |
||
|---|---|---|
Column |
Name |
Description |
1 |
VERSION |
Version number |
2 |
MODEL |
User provided text string giving model name |
3 |
DESC |
User provided text string describing the verification task |
4 |
FCST_LEAD |
Forecast lead time in HHMMSS format |
5 |
FCST_VALID |
Forecast valid time in YYYYMMDD_HHMMSS format |
6 |
OBS_LEAD |
Observation lead time in HHMMSS format |
7 |
OBS_VALID |
Observation valid time in YYYYMMDD_HHMMSS format |
8 |
T_DELTA |
Time separation between input data files in HHMMSS format |
9 |
FCST_T_BEG |
Forecast time convolution begin offset |
10 |
FCST_T_END |
Forecast time convolution end offset |
11 |
FCST_RAD |
Forecast convolution radius in grid units |
12 |
FCST_THR |
Forecast convolution threshold |
13 |
OBS_T_BEG |
Observation time convolution begin offset |
14 |
OBS_T_END |
Observation time convolution end offset |
15 |
OBS_RAD |
Observation convolution radius in grid units |
16 |
OBS_THR |
Observation convolution threshold |
17 |
FCST_VAR |
Forecast variable |
18 |
FCST_UNITS |
Units for forecast variable |
19 |
FCST_LEV |
Forecast vertical level |
20 |
OBS_VAR |
Observation variable |
21 |
OBS_UNITS |
Units for observation variable |
22 |
OBS_LEV |
Observation vertical level |
2D Attribute Columns |
||
|---|---|---|
Column |
Name |
Description |
23 |
OBJECT_ID |
Object number |
24 |
OBJECT_CAT |
Object category |
25 |
TIME_INDEX |
Time index of slice |
26 |
AREA |
2D cross-sectional area |
27 |
CENTROID_X |
x coordinate of centroid |
28 |
CENTROID_Y |
y coordinate of centroid |
29 |
CENTROID_LAT |
Latitude of centroid |
30 |
CENTROID_LON |
Longitude of centroid |
31 |
AXIS_ANG |
Angle that the axis makes with the grid x direction |
32 |
INTENSITY_10 |
\(\text{10}^{th}\) percentile intensity in time slice |
33 |
INTENSITY_25 |
\(\text{25}^{th}\) percentile intensity in time slice |
34 |
INTENSITY_50 |
\(\text{60}^{th}\) percentile intensity in time slice |
35 |
INTENSITY_75 |
\(\text{75}^{th}\) percentile intensity in time slice |
36 |
INTENSITY_90 |
\(\text{90}^{th}\) percentile intensity in time slice |
37 |
INTENSITY_* |
User-specified percentile intensity in time slice |
3D Single Attribute Columns |
||
|---|---|---|
Column |
Name |
Description |
23 |
OBJECT_ID |
Object number |
24 |
OBJECT_CAT |
Object category |
25 |
CENTROID_X |
x coordinate of centroid |
26 |
CENTROID_Y |
y coordinate of centroid |
27 |
CENTROID_T |
t coordinate of centroid |
28 |
CENTROID_LAT |
Latitude of centroid |
29 |
CENTROID_LON |
Longitude of centroid |
30 |
X_DOT |
x component of object velocity |
31 |
Y_DOT |
y component of object velocity |
32 |
AXIS_ANG |
Angle that the axis plane of an object makes with the grid x direction |
33 |
VOLUME |
Integer count of the number of 3D “cells” in an object |
34 |
START_TIME |
Object start time |
35 |
END_TIME |
Object end time |
36 |
CDIST_TRAVELLED |
Total great circle distance travelled by the 2D spatial centroid over the lifetime of the 3D object |
37 |
INTENSITY_10 |
\(\text{10}^{th}\) percentile intensity inside object |
38 |
INTENSITY_25 |
\(\text{25}^{th}\) percentile intensity inside object |
39 |
INTENSITY_50 |
\(\text{50}^{th}\) percentile intensity inside object |
40 |
INTENSITY_75 |
\(\text{75}^{th}\) percentile intensity inside object |
41 |
INTENSITY_90 |
\(\text{90}^{th}\) percentile intensity inside object |
42 |
INTENSITY_* |
User-specified percentile intensity inside object |
3D Pair Attribute Columns |
||
|---|---|---|
Column |
Name |
Description |
23 |
OBJECT_ID |
Object number |
24 |
OBJECT_CAT |
Object category |
25 |
SPACE_CENTROID_DIST |
Spatial distance between \((x,y)\) coordinates of object spacetime centroid |
26 |
TIME_CENTROID_DELTA |
Difference in t index of object spacetime centroid |
27 |
AXIS_DIFF |
Difference in spatial axis plane angles |
28 |
SPEED_DELTA |
Difference in object speeds |
29 |
DIRECTION_DIFF |
Difference in object direction of movement |
30 |
VOLUME_RATIO |
Forecast object volume divided by observation object volume |
31 |
START_TIME_DELTA |
Difference in object starting time steps |
32 |
END_TIME_DELTA |
Difference in object ending time steps |
33 |
INTERSECTION_VOLUME |
“Volume” of object intersection |
34 |
DURATION_DIFF |
Difference in the lifetimes of the two objects |
35 |
INTEREST |
Total interest for this object pair |
NetCDF File
MTD writes a NetCDF file containing various types of information as specified in the configuration file. The possible output data are:
Latitude and longitude of all the points in the 2D grid. Useful for geolocating points or regions given by grid coordinates.
Raw data from the input data files. This can be useful if the input data were grib format, since NetCDF is often easier to read.
Object ID numbers, giving for each grid point the number of the simple object (if any) that covers that point. These numbers are one-based. A value of zero means that this point is not part of any object.
Cluster ID numbers. As above, only for cluster objects rather than simple objects.